[3]DCTは、元画像を圧縮しやすくする変換技術
[3]DCTは、元画像を圧縮しやすくする変換技術
(1)画素の関係を周波数の関係に変換
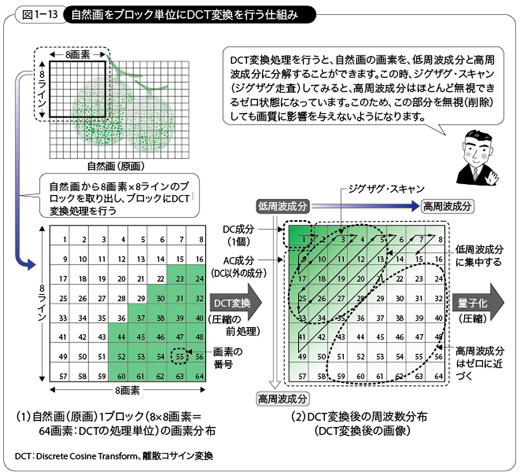
前述したようにDCTは、入力されるアナログの元画像を、数学的な離散コサイン変換という手順(アルゴリズムとも言われる)を用いて低周波や高周波などの周波数成分に分解する仕組みをもっている変換技術なのです。すなわち、図1-13に示すように、画面の中の「画素の関係」(画素領域と言う)を、「周波数の関係」(周波数領域と言う)に変換し、これによって元画像を圧縮しやすくしています。これは、前述した「A」という文字をデジタル情報の「10010」という別の情報に変換した手法と同じように、「画素」を別の情報である「周波数」に変換して、圧縮をしやすくしているのです。
一般に、人間の眼の視覚特性は、低周波成分に敏感(情報を削減するとかなり感じる)であり、高周波成分には鈍感(情報を削減してもあまり感じない)であるため、このような特性を利用するうえでも、DCTは好都合です。
DCTの場合は、DCT変換して得られた周波数成分の値を逆に変換する、すなわち逆DCTの変換をすることによって、完全に元の画素値に戻すことができます。すなわち、DCTで変換(周波数分解)した結果は、画像の表現方法を「画素ブロックから周波数成分」に変えただけであり、当然のことながら圧縮処理は何もしていないので、元の画像に含まれていた情報はすべて保存されています(可逆的な処理)。
(2)DCT係数はDC成分とAC成分で構成
なお、画像にDCTを適用して変換(周波数分解)した結果の数値は、「DCT係数」と言われます。DCT係数は、図1-13(2)に示すように、直流(DC:Direct Current)成分と交流(AC:Alternate Current)成分から構成されています。
DC成分とは、値が変化しない成分、すなわち周波数が最も低い「ゼロ」のところの係数です。このDC成分以外は、低周波から高周波に至るまですべて値の変化があるAC成分です。自然画像は、なだらかであり変化が少ないので、高周波成分はあまり含まれていません。そこで、例えばAC係数の中でも高周波成分に相当するAC係数を削除(その部分のAC係数をゼロと見なしてしまう)し、情報を圧縮することができます。
このように、DCTで変換した情報(すなわちDCT係数)の中には、冗長な情報(削除しても画質に影響を与えない情報。例:高い周波成分)も含まれていますので、DCT変換した結果(DCT係数)の情報から、冗長な情報を除去することが容易になります。
実際、多くの自然画をDCTで変換すると、周波数成分のほとんど(ほとんどのDCT係数)が低周波領域に集中し(かたよる)、高周波成分は無視できる(高周波成分のDCT係数はほとんどゼロになる)状況が生まれるため、高周波成分を削除しても画質に影響しないことになります。したがって、この高周波成分を削除することによって、画像情報を圧縮できるようになります。ここで、DCTという変換技術は、あくまでも画像を圧縮しやすくするための変換技術であり、圧縮技術そのものではないことに注意してください。
一般に、自然画像の画素値の周波数分布は、低域(低周波領域)に集中しているため、画像圧縮符号化にDCT変換を適用すると、大きな圧縮効果を発揮するのです。
[4]DCTの原理を「野球のチーム」の例で理解する
思い切ったたとえとして、野球のチームを考えてみましょう。野球チームは9人以上の選手で構成され、選手の氏名の集まりで表現できます。同様に選手の背番号でも表現できます。多くの場合、高校野球などでは選手の数は多くても、有力な選手は「小さい数字の背番号」(前述の低周波成分に相当)をつけていますので、背番号が若番の選手を集めればほぼそのチームを表しています。このように選手の氏名を背番号に変換することによって、簡潔にチームを言い表す道が開けます。
変換という言葉は一般的な数学処理の呼び名ですが、その変換の具体的な方法の一つであるDCTは、デジタル処理と画像の性質に適合した変換です。この変換の処理には、多くの積和演算(掛け算と足し算)が必要です。そのため、信号処理用のLSIやCPUの処理能力が向上した1980年代中頃になって、画像圧縮のための変換の処理が初めて実用的になりました。
次回は「【基本要素4】変換:DCT(離散コサイン変換)」について説明します。
※この「Q&Aで学ぶ基礎技術:最新の情報圧縮技術〔H.264/AVC〕編」は、著者の承諾を得て、好評発売中の「改訂版 H.264/AVC教科書」の第1章に最新情報を加えて一部修正し、転載したものです。ご了承ください。
バックナンバー
筆者の人気記事

Q&Aで学ぶH.264/AVC(12):圧縮技術の基本的な技術「DCT(離散コサイン変換)」とは?
2008年7月14日 0:00

Q&Aで学ぶH.264/AVC(4):情報をデジタル化する仕組みは?
2008年3月4日 0:00

Q&Aで学ぶH.264/AVC(1):H.264とは? AVCとは?
2008年2月25日 0:00

Q&Aで学ぶH.264/AVC(11):圧縮技術の基本的な要素は?
2008年7月7日 0:00

Q&Aで学ぶH.264/AVC(13):圧縮技術の基本的な技術「可変長符号化方式」の特徴とは?
2008年7月18日 0:00

Q&Aで学ぶH.264/AVC(6):ハイビジョンでも使われる「色差信号」とは?
2008年3月17日 0:00