送電網シミュレータから微分解析機へ
ブッシュは1919年、ジャクソンに招かれてMITの準教授になり、送電網の講義と大学院生の指導を担うことになった。ブッシュはMITで、送電網の安定性の問題に取り組み、1923年、必要な微分積分をエンジニアが簡単に扱える代数式に変換する方法を、「実働回線分析（Operational Circuit Analysis）」という著作にまとめた。ブッシュはこれにより同年、教授に昇格した。
1924年、GEがカナダから米国北東部に全長800kmの送電網の敷設計画を発表すると、ブッシュはそのミニチュア版を設計する計画を立てた。翌年、8つの発電機と40の変電所を60の回線で結ぶ送電網を、変圧器とコンデンサとケーブルで形成し、中央にプラグボードを配置して様々な電力網を構成することに成功。ブッシュはこの送電網シミュレータで、短期的な異常現象を発生させて測定し、電力網全体に与える影響を計算しようとした。
しかし、ブッシュは繰り返し計算に忙殺された。そこで、送電網の現象を表す微分方程式を、直接評価する方法を考えるようになった。ブッシュはプロファイル・トレーサーに応用した積分器を用いて、計算機が設計できるか検討を重ねた。積分器は、複雑な曲線に囲まれた図形の面積を測定するプラニメーター(planimeter)を実現するために、1836年に考案され、1878年に実用的な器具が開発されていた。
積分器のディスクは可動台で、水平方向にスライドさせることができ、円盤の位置をディスクの中心と縁の間に設定することができる。円盤の回転は中心に近ければ遅く、縁に近づくにつれ速くなり、円盤の回転数は y の距離に比例して変化する。ディスクの回転を x、ディスクの中心から車輪の位置までの距離を y とすると、車輪の回転が積分の値を表す。
プラニメーターで閉曲線内の面積を求める場合、y軸上の点aとbの間の曲線は、関数f(y)の積分なので、S=∫baf(y)dyで解くことができる。y=f(x)のグラフであれば、z=∫f(x)dxと書き換えて答えが得られる。そして、2つの積分機を連結すると、2つの関数を扱うことができ、f(y)=∫f(y)g(y)dy に相当する微分方程式を解くことができる。
しかし、ディスクの摩擦で回転する円盤のトルク（回転力）は極めて弱く、他の装置を駆動することが難しい。1927年にベツレヘム・スティールが、自動車のパワーステアリングを実現する「ベツレヘム・トルクアンプ」を発表すると、ブッシュはこのアイデアで積分器のトルクを増強できると考え、1928年に微分解析機のプロジェクトを開始した。
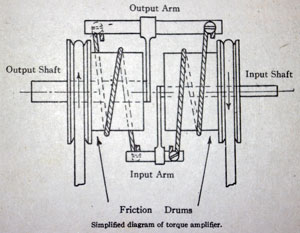
写真1 トルクアンプの設計図
（提供：東京理科大学 近代科学資料館 ）
トルクアンプは、ハンドルの回転を忠実に再現する装置だが、モーターとベルトでドラムを締め上げて回転を伝えることにより、トルクを大幅に引き上げ、トラックなどの巨大な車輪を操縦できるようにした。ブッシュは同じ仕組みで積分器のトルクを1万倍にして、多数の積分器と入出力装置を連動できるようにした。
微分解析機は、入力テーブルにグラフを描き、出力テーブルに計算結果をグラフで表示する。入力テーブルのグラフを入力ポインタでなぞると、連結するバス・ロッドの位置を決めることができる。最初の微分解析機には18本のロッドが格子状に配備され、格子の交点に配備したらせん状のギアを入れた連結器に、4本のロッドを接続して回転を伝えていた。ロッドの位置とギア比の組み合わせで必要な変数の初期値を設定し、ロッドの回転が変数を積分器に伝える仕組みになっていた。
ブッシュは1931年、6つの積分器と3つの入力テーブル、1つの出力テーブル、および手動の乗算機で構成された微分解析機の1号機を、2万5千ドルで完成させた。この微分解析機は6階の常微分方程式を扱うことができた（写真2、3）。
写真2 微分解析機の前に立つバネバー・ブッシュ
（Photo: Courtesy MIT Museum）(クリックで拡大)
写真3 ブッシュの論文を参考にして1930年代に日本で作られた微分解析機（東京理科大学 近代科学資料館 所蔵）(クリックで拡大)
